Uma nova geometria para estudar espaço curvo descrito por Einstein

Com informações do JQI - 05/02/2021

Esta é uma representação de uma grade de heptágonos em um espaço hiperbólico. Para ajustar a grade hiperbólica uniforme em um espaço "plano", o tamanho e a forma dos heptágonos ficam distorcidos. No espaço hiperbólico apropriado, cada heptágono teria forma e tamanho idênticos, em vez de ficar menores e mais distorcidos nas bordas.
[Imagem: Kollár et al.]

Espaço curvo

Einstein nos mostrou que o nosso espaço tridimensional se curva, o que torna o tempo relativo, criando uma arquitetura na qual as duas coisas se mesclam, o espaço-tempo.

O problema é, quando nos propomos a estudar esse espaço curvo, todas as nossas ferramentas de geometria, desenvolvidas para o que agora chamamos de "espaço Euclidiano", mostram-se inúteis.

Acontece que o espaço conforme descrito por Einstein, que agora conhecemos como não-Euclidiano, apresenta paisagens desconcertantes: O espaço pode se contrair, de modo que linhas retas e paralelas se juntam, em vez de manter um espaçamento fixo; ou pode expandir-se fazendo essas linhas se distanciarem cada vez mais, para sempre. Nesses mundos, quatro ruas de comprimento igual, todas conectadas por curvas à direita em ângulos retos, podem não formar um quarteirão quadrado que o leve à sua esquina inicial.

Os físicos estão interessados em estudar o espaço curvo porque ele pode revelar "novas físicas", e as geometrias não-Euclidianas podem até ajudar a melhorar algumas tecnologias.

Espaço hiperbólico

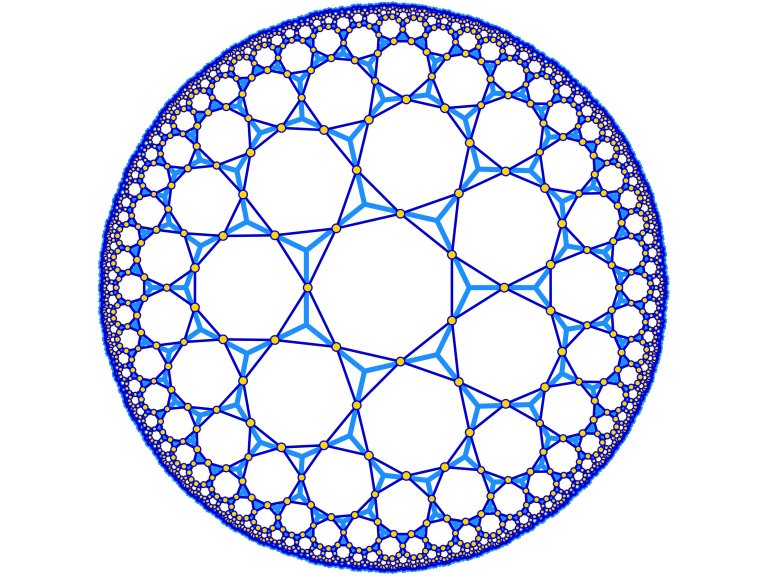
Um tipo de geometria não-Euclidiana particularmente interessante é o espaço hiperbólico, também chamado de espaço com curvatura negativa.

Mesmo uma versão física bidimensional de um espaço hiperbólico é impossível de ser feita em nosso ambiente "plano" normal. Mas os cientistas ainda podem imitar ambientes hiperbólicos para explorar como certas físicas atuam em espaços com curvaturas negativas.

No ano passado, a equipe da professora Alicia Kollár, da Universidade de Maryland, nos EUA, criou um chip que simula o espaço curvo, permitindo estudar de partículas a buracos negros.

Agora eles criaram uma nova caixa de ferramentas matemáticas que permite entender melhor essas simulações do espaço hiperbólico.

Eles chamam as ferramentas de "dicionário entre a geometria discreta e a geometria contínua", afirmando que ela irá ajudar os pesquisadores a traduzir os resultados experimentais em uma forma mais útil e mais inteligível, permitindo explorar melhor o mundo às avessas do espaço hiperbólico.

Esquema do chip que simula o espaço curvo desenvolvido pela equipe.
[Imagem: Kollár et al. - 10.1038/s41586-019-1348-3]

"Muita física legal"

Kollár brinca que a situação não é exatamente como Alice caindo na toca do coelho, mas que esses experimentos são uma oportunidade para explorar um novo mundo, onde descobertas surpreendentes podem estar se escondendo atrás de qualquer esquina - e onde o próprio significado de virar uma esquina precisa ser reconsiderado.

"Existem realmente muitas aplicações para esses experimentos," disse seu colega Igor Boettcher. "Neste ponto, é impossível prever tudo o que pode ser feito, mas espero que [as ferramentas] tenham muitas aplicações ricas e muita física legal."

Como exemplo dessa "física legal", Boettcher cita o estudo da correspondência AdS/CFT (sigla em inglês para espaço anti-de-Sitter/teoria do campo conformal), também conhecida como a conjectura de Maldacena, uma conjectura da física para combinar as teorias da gravidade quântica e as teorias de campo quântico usando uma descrição não-Euclidiana do Universo.

E Kollár planeja explorar se esses experimentos podem revelar ainda mais física ao incorporar interações nas simulações do seu chip.

Mais tópicos