Física explica enigma da Matemática, a Hipótese de Riemann
Redação do Site Inovação Tecnológica - 24/11/2021
[Imagem: Sissa]
Hipótese de Riemann
O fato de a matemática fornecer à física a linguagem certa para formular as leis da natureza está na própria lógica das coisas.
Mas a possibilidade de que a física forneça a chave para a compreensão de um genuíno mistério da matemática é, ao contrário, um fato bastante incomum e extraordinário.
Mas é o que parece estar acontecendo agora, pela primeira vez.
No centro das atenções está a famosa hipótese de Riemann - ou conjectura de Riemann -, um dos problemas mais famosos da matemática.
Em 1859, o matemático alemão Bernhard Riemann [1826-1866] publicou um artigo que mudaria a história da matemática. O artigo dizia respeito ao mistério dos números primos e à possibilidade de prever sua distribuição enigmática com uma precisão surpreendente.
Infinitos zeros ao longo de uma linha vertical
"No cerne do argumento de Riemann havia uma conjectura, que ele não foi capaz de provar, sobre a localização de um número infinito de zeros no plano complexo de uma função particular, conhecida como função de Riemann. Esses zeros parecem se alinhar magicamente ao longo de uma linha vertical com uma abscissa exatamente igual a 1/2, e até agora ninguém conseguiu entender a razão de uma regularidade tão incrível," explicou Giuseppe Mussardo, da Escola Internacional de Estudos Avançados, na Itália.
Agora, ele e seu colega André Leclair demonstraram que há uma explicação extremamente elegante do alinhamento dos zeros ao longo do eixo 1/2 da função de Riemann - bem como de infinitas funções semelhantes, as chamadas funções de Dirichlet.
Segundo a dupla, essa distribuição se deve, em última análise, a um motivo totalmente inesperado: À presença de um movimento caótico e às leis de probabilidade que regem esse movimento.
Na verdade, Mussardo e Leclair provaram a existência de um movimento browniano oculto por trás de todas essas funções infinitas.
É uma reviravolta surpreendente, uma espécie de reciprocidade, ou simetria no conhecimento: Há pouco tempo, os físicos mostraram que a função de onda, que explica as partículas atômicas e subatômicas, é uma matemática que virou realidade. Agora, os matemáticos mostraram que um movimento aleatório das partículas explica a presença de um padrão na matemática.
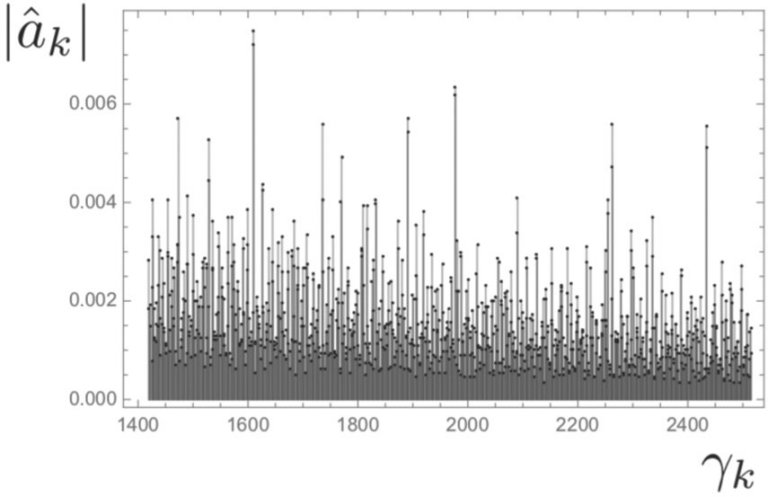
[Imagem: Giuseppe Mussardo et al. - 10.1088/1742-5468/ac22fb]
Movimento browniano explicando hipótese de Riemann
O movimento browniano, fenômeno-chave na mecânica estatística, e explicado pela primeira vez por Albert Einstein em 1906, é o movimento caótico e desordenado dos átomos de um gás devido à altíssima frequência de suas colisões.
No movimento browniano, 1/2 é o expoente universal que rege como os átomos se espalham com o passar do tempo, um expoente incrivelmente robusto devido às leis probabilísticas descobertas pelo Carl Friedrich Gauss [1777-1855], fazendo parte do seu famoso teorema do limite central (Quando o tamanho de uma amostra aumenta, a distribuição amostral da sua média aproxima-se cada vez mais de uma distribuição normal, ou distribuição de Gauss).
"Nossa hipótese sobre a natureza browniana da conjectura de Riemann, amparada em uma série de resultados probabilísticos que provamos na Teoria dos Números, foi acompanhada por uma análise estatística maciça e extremamente precisa feita ao longo da sequência infinita de números primos, uma verdadeiro façanha que nos manteve ocupados por cerca de três anos," contou Mussardo.
"O fato de a explicação da conjectura de Riemann vir da física, ou seja, da mecânica estatística, e as surpreendentes conexões desse campo com um tema genuinamente matemático, como a teoria dos números, revela ao mesmo tempo a grande unidade do conhecimento científico e, ao mesmo tempo, aumenta nosso espanto diante de um fato tão profundo," concluiu a dupla em ser artigo.
De fato, matemáticos e físicos deverão se deleitar com este trabalho, mas suas implicações mais profundas ficarão provavelmente por conta da filosofia da ciência.
Artigo: Randomness of Möbius coefficients and Brownian motion: growth of the Mertens function and the Riemann hypothesis
Autores: Giuseppe Mussardo, André LeClair
Revista: Journal of Statistical Mechanics Theory and Experiment
Vol.: 2021, 113106
DOI: 10.1088/1742-5468/ac22fb


Ar-condicionado verde e de estado sólido alcança escala de quilowatts
Constantes fundamentais da natureza garantem supercondutores a temperatura ambiente
Água líquida não é única: São dois líquidos diferentes
Algo do nada: Físicos resfriam objeto medindo... nada
Eletricidade é gerada usando rotação da Terra em seu próprio campo magnético
Lançado um "linux" para computadores quânticos
Medição que contesta teoria da física é revalidada
Energia escura não é o que pensamos, o que muda nossa visão do Universo
Rival dos computadores quânticos tem avanço revolucionário
Lançado computador quântico de silício pronto para ser plugado na tomada
Simulação reforça indícios da existência do Planeta 9
Buracos negros podem fomentar a vida galáxia afora
Gravidade pode emergir da entropia, e não da curvatura do espaço-tempo
Água líquida não é única: São dois líquidos diferentes
E se buracos negros forem o começo, e não o fim de algo?
Constantes fundamentais da natureza garantem supercondutores a temperatura ambiente
Todos os direitos reservados.
É proibida a reprodução total ou parcial, por qualquer meio, sem prévia autorização por escrito.




